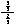Binomial Theorem

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power (x + y)n into a sum involving terms of the form ax^by^c, where the coefficient of each term is a positive integer, and the sum of the exponents of x and y in each term is n. For example,

The coefficients appearing in the binomial expansion are known as binomial coefficients. They are the same as the entries of Pascal's triangle, and can be determined by a simple formula involving factorials. These numbers also arise in combinatorics, where the coefficient of x^n−ky^k is equal to the number of different combinations of k elements that can be chosen from an n-element set.

The binomial coefficients appear as the entries of Pascal's triangle.

Statement of the Theorem

According to the theorem, it is possible to expand any power of x + y into a sum of the form
where

denotes the corresponding binomial coefficient. Using summation notation, the formula above can be written

This formula is sometimes referred to as the Binomial Formula or the Binomial Identity.

A variant of the binomial formula is obtained by substituting 1 for x and x for y, so that it involves only a single variable. In this form, the formula reads



or equivalently




Examples
The most basic example of the binomial theorem is the formula for square of x + y:

The binomial coefficients 1, 2, 1 appearing in this expansion correspond to the third row of Pascal's triangle. The coefficients of higher powers of x + y correspond to later rows of the triangle:

The binomial theorem can be applied to the powers of any binomial. For example,

For a binomial involving subtraction, the theorem can be applied as long as the negation of the second term is used. This has the effect of negating every other term of the expansion:

Formulas
The coefficient of x^n−ky^k is given by the formula

which is defined in terms of the factorial function n!. Equivalently, this formula can be written

with k factors in both the numerator and denominator of the fraction. Note that, although this formula involves a fraction, the binomial coefficient

is actually an integer.

Reference:
http://en.wikipedia.org/wiki/Binomial_theorem

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.

The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line. Given two points (x1,y1) and (x2,y2) on a line, the slope m of the line is

Through differential calculus, one can calculate the slope of the tangent line to a curve at a point.

The concept of slope applies directly to grades or gradients in geography and civil engineering. Through trigonometry, the grade m of a road is related to its angle of incline θ by




The slope of afined as the rise over the run, m = Δy/Δx.

The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. This is described by the following equation:

(The delta symbol, "Δ", is commonly used in mathematics to mean "difference" or "change".)

Given two points (x1,y1) and (x2,y2), the change in x from one to the other is x2 − x1 (run), while the change in y is y2 − y1 (rise). Substituting both quantities into the above equation obtains the following:

Slope illustrated for y = (3/2)x − 1.

Suppose a line runs through two points: P = (1, 2) and Q = (13, 8). By dividing the difference in y-coordinates by the difference in x-coordinates, one can obtain the slope of the line:


The slope is 0.5.

As another example, consider a line which runs through the points (4, 15) and (3, 21). Then, the slope of the line is


Using Slope and y-Intercept to Graph Lines

Given two points (x1, y1) and (x2, y2), the formula for the slope of the straight line going through these two points is:

...where the subscripts merely indicate that you have a "first" point (whose coordinates are subscripted with a "1") and a "second" point (whose coordinates are subscripted with a "2"); that is, the subscripts indicate nothing more than the fact that you have two points to work with. Note that the point you pick as the "first" one is irrelevant; if you pick the other point to be "first", then you get the same value for the slope:

The formula for slope is sometimes referred to as "rise over run", because the fraction consists of the "rise" (the change in y, going up or down) divided by the "run" (the change in x, going from left to the right). If you've ever done roofing, built a staircase, graded landscaping, or installed gutters or outflow piping, you've probably encountered this "rise over run" concept. The point is that slope tells you how much y is changing for every so much that x is changing. Pictures can be helpful, so let's look at the line y = ( 2/3 )x – 4; we'll compute the slope, and draw the line.

To find points from the line equation, we have to pick values for one of the variables, and then compute the corresponding value of the other variable. If, say, x = –3, then y = ( 2/3 )(–3) – 4 = –2 – 4 = –6, so the point (–3, –6) is on the line. If x = 0, then y = ( 2/3 )(0) – 4 = 0 – 4 = –4, so the point (0, –4) is on the line. Now that we have two points on the line, we can find the slope of that line from the slope formula:

Let's look at these two points on the graph:














In stair-stepping up from the first point to the second point, our "path" can be viewed as forming a right triangle:

The distance between the y-values of the two points (that is, the height of the triangle) is the "y2 – y1" part of the slope formula. The distance between the x-values (that is, the length of the triangle) is the "x2 – x1" part of the slope formula. Note that the slope is 2/3, or "two over three". To go from the first point to the second, we went "two up and three over". This relationship between the slope of a line and pairs of points on that line is always true.

To get to the "next" point, we can go up another two (to y = –2), and over to the right another three (to x = 3):
With these three points, we can graph the line y = ( 2/3 )x – 4.

Let's try another line equation: y = –2x + 3. We've learned that the number on x is the slope, so m

= –2 for this line. If, say, x = 0, then y = –2(0) + 3 = 0 + 3 = 3. Then the point (0, 3) is on the line. With this information, we can find more points on the line. First, though, you might want to convert the slope value to fractional form, so you can more easily do the "up and over" thing. Any number is a fraction if you put it over "1", so, in this case, it is more useful to say that the slope is m = –2/1. That means that we will be going "down two and over one" for each new point.

We'll start at the point we found above, and then go down two and over one to get to the next point:














Go down another two, and over another one, to get to the "next" point on y = –2x + 3:














Given a point on the line, you can use the slope to get to the "next" point by counting "so many up or down, and then so many over to the right". But how do you find your first point? Take a look back at the graph of the first line and its equation: y = ( 2/3 )x – 4 crossed the y-axis at y = –4, so the equation gave us the y-intercept. The second line did too: the graph of y = –2x + 3 crossed the y-axis at y = 3. This relationship always holds true: in y = mx + b, "b" gives the y-intercept, and "m" is the slope. We can use this fact to easily graph straight lines:

Graph the equation y = ( 3/5 ) x – 2 from the slope and y-intercept.
From the equation, I know that the slope is m = 3/5, and that the line crosses the y-axis at
y = –2.

I'll start by plotting this first point:












From this point, I go up three and over five:












Then I go up another three and over another five to get my third point:












With three points, I can draw my line:














Reference:
http://en.wikipedia.org/wiki/Slope
http://www.purplemath.com/modules/slopgrph2.htm

Simplifying with Parentheses

When simplifying expressions with parentheses, you will be applying the Distributive Property. That is, you will be distributing over (multiplying through) a set of parentheses in order to simplify a given expression. I will walk you through some examples of increasing difficulty, and you should note, as this lesson progresses, the importance of simplifying as you go and of doing each step neatly, completely, and exactly.

Simplify 3(x + 4).

To "simplify" this, I have to get rid of the parentheses. The Distributive Property says to multiply the 3 onto everything inside the parentheses. I sometimes draw arrows to emphasize this:

Then I multiply the 3 onto the x and onto the 4:
3(x) + 3(4)

3x + 12

Written all in one line, this would look like:

The most common error at this stage is to take the 3 through the parentheses but only onto the x, forgetting to carry it through onto the 4 as well. If you need to draw little arrows to help you remember to carry the multiplier through onto everything inside the parentheses, then use them!

Simplify –2(x – 4)
I have to take the –2 through the parentheses. This gives me:

–2(x – 4)
–2(x) – 2(–4)
–2x + 8

The common mistake students make with this type of problem is to lose a "minus" sign somewhere, such as doing "–2(x – 4) = –2(x) – 2(4) = –2x – 8". Did you notice how the "–4" somehow turned into a "4" when the –2 went through the parentheses? That's why the answer ended up being wrong. Be careful with the "minus" signs! Until you are confident in your skills, take the time to write out the distribution, complete with the signs, as I did.

–2(x – 4)
–2(x) – 2(–4)
–2x + 8

If you have difficulty with the subtraction, try converting it to addition of a negative:

–2(x – 4)
–2(x + [–4])
–2(x) + (–2)(–4)
–2x + 8

Do as many steps as you need to, in order to consistently get the correct answer.

Simplify –(x – 3)

I have to take the "minus" through the parentheses. Many students find it helpful to write in the little understood "1" before the parentheses:

–1(x – 3)

I need to take a –1 through the parentheses:

–(x – 3)
–1(x – 3)
–1(x) – 1(–3)
–1x + 3
–x + 3

Note that "–1x + 3" and "–x + 3" are technically the same thing; in my classes, either would be a perfectly acceptable answer. However, some teachers will accept only "–x + 3" and would count

"–1x + 3" as not fully simplified. It would be wise to check with your instructor, especially if you find it helpful to write in that understood "1".

Simplify 2 + 4(x – 1)

The order of operations tells me that multiplication comes before addition. I can't do the "2 + " until I have taken the 4 through the parentheses.

2 + 4(x – 1)
2 + 4(x) + 4(–1)
2 + 4x + (–4)
2 – 4 + 4x
–2 + 4x
4x – 2

I would accept either of "4x – 2" and "–2 + 4x" as a valid answer. However, most texts expect the answer to be written in "descending order" (with the variable term first, and then the plain number). You should know that the two expressions of the answer are the same, but that some instructors insist that the answer be written in descending order. It would probably be best to get in the habit now of writing your answers in descending order.

Parentheses inside of parentheses are called "nested" parentheses. The process of simplification works the same way as in the simpler examples on the previous page, but you do need to be a little more careful as you work your way through the grouping symbols.

Simplify 4[x + 3(2x + 1)]

With nested parentheses like this, the safest plan is to work from the inside out. So I'll take the 3 through the inner parentheses first, before I even think about dealing with the 4 and the square brackets. I'll also simplify as much as I can as I go along. Note that I write each step out completely as I go:

4[x + 3(2x + 1)]
4[x + 3(2x) + 3(1)]
4[x + 6x + 3]
4[7x + 3]
4[7x] + 4[3]
28x + 12

FYI: The traditional sequence of grouping symbols, working from the inside out, is "parentheses", then "brackets", and then "braces"; then you repeat the sequence, as necessary. But this is not, to my knowledge, a rule; it's just a common convention.

Simplify 9 – 3[x – (3x + 2)] + 4

I won't do anything with the "9 –" or the "+ 4" until I simplify inside the brackets and parentheses. I'll work from the inside out:

9 – 3[x – (3x + 2)] + 4
9 – 3[x – 1(3x + 2)] + 4
9 – 3[x – 1(3x) – 1(2)] + 4
9 – 3[x – 3x – 2] + 4
9 – 3[–2x – 2] + 4
9 – 3[–2x] – 3[–2] + 4
9 + 6x + 6 + 4
6x + 19

It is not required that you write out this many (or this few) steps. You should be careful to do one step at a time, though, writing things out completely and simplifying as you go. You should do as many steps as you need in order to consistently arrive at the correct answer.

Simplify 5 + 2{ [3 + (2x – 1) + x] – 2}
I'll work carefully from the inside out:

5 + 2{ [3 + (2x – 1) + x] – 2}
5 + 2{ [3 + 2x – 1 + x] – 2}
5 + 2{ [2x + x + 3 – 1] – 2}
5 + 2{ [3x + 2] – 2}
5 + 2{3x + 2 – 2}
5 + 2{3x}
5 + 6x
6x + 5

Reference:
http://www.purplemath.com/modules/simparen2.htm

Probability

Probability is a way of expressing knowledge or belief that an event will occur or has occurred. The concept has been given an exact mathematical meaning in probability theory, which is used extensively in such areas of study as mathematics, statistics, finance, gambling, science, and philosophy to draw conclusions about the likelihood of potential events and the underlying mechanics of complex systems.

Let's see how it could be defined on the simplest sample space of a single coin toss, {H, T}.

The two element sample space {H, T} has four subsets:

Φ = {}, {H}, {T}, {H, T} = Ω.

To be a probability, a function P defined on this four sets must be non-negative and not exceeding 1. In addition, on the two fundamental sets Φ and Ω it must take on the prescribed values:

P(Φ) = 0 and P(Ω) = 1.

The values P({H}) and P({T}) which we shall write more concisely as P(H) and P(T) must be somewhere in-between. P(H) is expected to be the probability of a coin landing heads up; P(T) should be the probability of its landing tails up. This is up to us to assign those probabilities. Intuitively those numbers should be expressing our notion of certainty with which the coin lands one way or the other. Since, for a fair coin, there is no way to prefer one side to the other, the most natural and common way is to make the two probabilities equal:

(1) P(H) = P(T).

As in real life, the choices we make have consequences. Once we decided that the two probabilities are equal, we are no longer at liberty to choose their common value. The definitions take over and dictate the result. Indeed, the two events {H} and {T} are mutually exclusive so that a probability function should satisfy the additivity requirement:

(2)

P({H}) + P({T}) = P({H} {T})

= P({H, T})

= P(Ω)

= 1.

The combination of (1) and (2) leads inevitably to the conclusion that a probability function that models a toss of a fair coin is bound to satisfy P(H) = P(T) = 1/2.

Two events that have equal probabilities are said to be equiprobable. It's a common approach, especially in the introductory probability courses, to define a probability function on a finite sample space by declaring all elementary events equiprobable and building up the function using the additivity requirement. Having a formal definition of probability function avoids the apparent circularity of the construction hinted at elsewhere.

Let's consider the experiment of rolling a die. The sample space consists of 6 possible outcomes

{1, 2, 3, 4, 5, 6}

which, with no indication that the die used is loaded, are declared to be equiprobable. From here, the additivity requirement leads necessarily to:

P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 1/6.

Since all 6 elementary events - {1}, {2}, {3}, {4}, {5}, {6} - are mutually exclusive, we may readily apply the required additivity, for example:

P({1, 2}) = P({1}) + P({2}) = 1/6 + 1/6 = 1/3

and similarly

P({4, 5, 6}) = P({4}) + P({5}) + P({6}) = 1/6 + 1/6 + 1/6 = 1/2

Note that a 2-element event {1, 2} has the probability of 1/3 = 2·1/6, whereas a 3-element event {4, 5, 6} has the probability of 1/2 = 3·1/6.

Let X be the random variable associated with the experiment of rolling the dice. The introduction of a random variable allows for naming various sets in a convenient manner, e.g.,:

{1, 2} = {x: x <> 3) = 1/2.

Here are a few additional examples:

P({2, 4, 6}) = P(X is even) = 1/2,

P({1, 2, 4, 5}) = P(X is not divisible by 3) = 2/3,

P({2, 3, 5}) = P(X is prime) = 1/2.

In general, if an event A has m favorable elementary outcomes, the additivity requirement implies P(A) = m/6. In other experiments, with n possible equiprobable elementary outcomes, we would have P(A) = m/n.

For example, under normal circumstances, drawing a particular card from a deck of 52 cards is assigned a probability of 1/52. Drawing a named (A, K, Q, J) card (of which there are 4×4 = 16 cards) has a probability of 16/52. The event of drawing a black card has the probability of 26/52 = 1/2, that of drawing a hearts the probability of 13/52 = 1/4 and the probability of drawing a 10 is 4/52 = 1/13.

Later on, we shall have examples of sample spaces where considering the elementary events as equiprobable is unjustified. However, whenever this is possible, the evaluation of probabilities becomes a combinatorial problem that requires finding the total number n of possible outcomes and the number m of the outcomes favorable to the event at hand. It is then natural that properties of combinatorial counting have bearings on the assignment and evaluation of probabilities.

When tossing two distinct (say, first and second) coins there are four possible outcomes {HH, HT, TH, TT} and no reason to declare one more likely than another. Thus each event is assigned the probability of 1/4. Here are more examples

P({H popped up at least once}) = P({HH, HT, TH}) = 3/4,

P(First coin came up heads) = P({HH, HT}) = 2/4 = 1/2,

P(Two outcomes were different) = P({HT, TH}) = 2/4 = 1/2.

We consider tossing two coins as completely independent experiments, the outcome of one having no effect on the outcome of the other. It follows then from the Sequential, or Product, Rule that the size of the sample space of the two experiments is the product of the sizes of the two sample spaces and the same holds of the probabilities. For example,

P({HT}) = 1/4 = 1/2·1/2 = P({H})·P({T}).

More generally, given two sample spaces S1 and S2 with the number of equiprobable outcomes n1 and n2 and two events E1 (on S1) and E2 (on S2) with the number of favorable outcomes m1 and m2. Then P(E1) = m1/n1 and P(E2) = m2/n2. The sample space of two successive experiments has a sample space with n1n2 outcomes. The event E1E2 which occurs if E1 took place followed by E2 taking place consists of m1m1 favorable outcomes so that

P(E1E2) = m1m2/n1n2 = m1/n1 · m2/n2 = P(E1)P(E2).

The two coins may be indistinguishable and, when thrown together, may produce only three possible outcomes {{H, H}, {H, T}, {T, T}} where the set notations are used to emphasize that the order of the outcomes of the two coins is irrelevant in this case. However, assigning each of the elementary events the probability of 1/3 is probably a bad choice. A more reasonable assignment is

P({H, H}) = 1/4,

P({H, T}) = 1/2,

P({T, T}) = 1/4.

Why? This is because the results of the two experiments won't change if we imagine the two coins different, say if we think of them as being blue and red. But, for different coins, the number of elementary events is 4, with two of them - HT and TH - destined to coalesce into one - {H, T} - when we back off from our fantasy. The other two - HH and TT - will still have the probabilities of 1/4 and the remaining total of 1/2 should be given to {H, T}.

When rolling two die, the sample space consists of 36 equiprobable elementary events each with probability 1/36. The possible sums of the two die range from 2 through 12 and the number of favorable events can be observed from the table below:

Using S for the random variable equal to the sum of the two die, the additivity requirement leads to the following probabilities:

P(S = 2) = 1/36,

P(S = 3) = 2/36 = 1/18,

P(S = 4) = 3/36 = 1/12,

P(S = 5) = 4/36 = 1/9,

P(S = 6) = 5/36,

P(S = 7) = 6/36 = 1/6,

P(S = 8) = 5/36,

P(S = 9) = 4/36 = 1/9,

P(S = 10) = 3/36 = 1/12,

P(S = 11) = 2/36 = 1/18,

P(S = 12) = 1/36,

Note that the events are mutually exclusive and exhaustive: their probabilities add up to 1.

(As a curiosity, note that, say, both sums of 4 and 5 come up in two ways, viz., 4 = 1 + 3, 4 = 2 + 2, 5 = 1 + 4, and 5 = 2 + 3. However, as we just saw, P(S = 4) < s =" 5).">

Let's return to throwing a dice. (For an historic example, see the Chevalier de Méré's Problem.) With 3 die, the sample space consists of 8 = 23 possible outcomes. Four 4 die the number grows to 16 = 24, and so on. We obtain a curious sample space tossing the coin until the first tail comes up. The probability P(T) that it will happen on the first toss equals 1/2. The probability P(HT) that it will happen on the second toss is evaluated under the assumption that the first toss showed heads, for, otherwise, the experiment would have stopped right after the first stop. The the outcome of the first toss has no effect on the outcome of the second,

P(HT) = P(H)·P(T) = 1/2 · 1/2 = 1/4.

Continuing in this way, P(HHT) = 1/2·1/2·1/2 = 1/8 is the probability of getting the tails on the third toss; P(HHHT) = 1/16 is the probability of getting the tails on the fourth toss, and so on. The events are mutually exclusive and exhaustive:

P(T) + P(HT) + P(HHT) + ... = 1/2 + 1/4 + 1/8 + ...

= 1/2·1 / (1 - 1/2)

= 1,

as the sum of a geometric series starting at 1/2 with the factor also of 1/2.

This is a curiosity because there is one event that has been left over: this is the event in which the outcome T never occurs. An infinite number of coin tosses is called for, each with the outcome of heads: HHHH ... Although abstractedly this event is complementary to the possibility of having a tails in a finite number of steps, this event is practically impossible because it requires an infinite number of coin tosses. Deservedly it is assigned the probability of 0.

The probability that tails will show up in four tosses or less equals

P(T) + P(HT) + P(HHT) + P(HHHT) = 1/2 + 1/4 + 1/8 + 1/16

= 1/2·(1 - 1/24)/ (1 - 1/2).

More generally, the probability that the tails will show up in at most n tosses equals to the sum

1/2 + 1/4 + 1/8 + ... + 1/2n = 1/2·(1 - 1/2n)/ (1 - 1/2).

The interpretation of the infinite sum 1/2 + 1/4 + 1/8 + ... is that this is the probability of the tails showing up in a finite number of steps. This probability is 1 so that one should expect to get the tails sooner or later. For this sample space, an event with probability 0 is conceivable but practically impossible. In continuous sample spaces, events with probability 0 are a regular phenomenon and far from being impossible.

The game of poker has many variants. Common to all is the fact that players get - one way or another - hands of five cards each. The hands are compared according to a predetermined ranking system. Below, we shall evaluate probabilities of several hand combinations.

Poker uses the standard deck of 52 cards. There are C(52, 5) possible combinations of 5 cards selected from a deck of 52: 52 cards to choose the first of the five from, 51 cards to choose the second one, ..., 48 to choose the fifth card. The product 52×51×50×49×48 must be divided by 5! because the order in which the five cards are added to the hand is of no importance, e.g., 7♣8♣9♣10♣J♣ is the same hand as 9♣7♣10♣J♣8♣. Thus there are C(52, 5) = 2598960 different hands. The poker sample space consists of 2598960 equally probable elementary events.

The probability of whichever hand is naturally 1/2598960. [Mazur, pp. 81-82] shows another elegant way of arriving at the same probability. Imagine having a urn with 52 balls, of which 5 are black and the remaining white. You are to draw 5 balls out of the urn. What is the probability that all 5 balls drawn are black?

The probability that the first ball is black is 5/52. Assuming that the first ball was black, the probability that the second is also black is 4/51. Assuming that the first two balls are black, the probability that the third is black is 3/50, ... The fifth ball is black with the probability of 1/48, provided the first 4 balls were all black. The probability of drawing 5 black balls is the product:

The highest ranking poker hand is a Royal Flush - a sequence of cards of the same suit starting with 10, e.g., 10♣J♣Q♣K♣A♣. There are 4 of them, one for each of the four suits. Thus the probability of getting a royal flush is 4/2598960 = 1/649740. The probability of getting a royal flush of, say, spades ♠, is of course 1/2598960.

Any sequence of 5 cards of the same suit is a straight flush ranked by the highest card in the sequence. A straight flush may start with any of 2, 3, 4, 5, 6, 7, 8, 9, 10 cards and some times with an Ace where it is thought to have the rank of 1. So there are 9 (or 10) possibilities of getting a straight flush of a given suit and 36 (or 40) possibilities of getting any straight flush.

Five cards of the same suit - not necessarily in sequence - is a flush. There are 13 cards in a suit and C(13, 5) = 1287 combinations of 5 cards out of 13. All in all, there are 4 times as many flush combinations: 5148.

Four of a kind is a hand, like 5♣5♠5♦5♥K♠, with four cards of the same rank and one extra, unmatched card. There are 13 combinations of 4 equally ranked cards each of which can complete a hand with any of the remaining 48 cards. Giving the total of 13×48 = 624 possible "four of a kind" combinations.

A hand with 3 cards of one rank and 2 cards of a different rank is known as Full House. For a given rank, there are C(4, 3) = 4 ways to choose 3 cards of that rank; there 13 ranks to consider. There are C(4, 2) = 6 combinations of 2 cards of equal rank, but now only 12 ranks to choose from. There are then 4×13×6×12 = 3744 full houses.

A straight hand is a straight flush without "flush", so to speak. The card must be in sequence but not necessarily of the same suit. If the ace is allowed to start a hand, there are 40 ways to choose the first card and then, we need to account that the remaining 4 cards could be of any of the 4 suits, giving the total of 40×4×4×4×4 = 10240 hands. Discarding 40 straight flushes leaves 10200 "regular" flushes.

Three of a kind is a hand, like 5♣5♠5♦7♥K♠, where three cards have the same rank while the remaining 2 differ in rank between themselves and the first three. There are 13×C(4, 3) = 52 combinations of three cards of the same rank. The next card could be any of 48 and the fifth any of 44 and the pair could come in any order so the products needs to be halved: 52×48×44 / 2 = 54912.

There remain Two pair and One pair combinations that are left as an exercise.

Reference;
http://www.cut-the-knot.org/probability.shtml
http://en.wikipedia.org/wiki/Probability

Signed Numbers

Signed Numbers

Positive numbers are the result of any measurement -- in length, weight, volume, loudness, etc. Negative numbers are the result of any measuring process in which a certain zero point is reached. For example, a temperature of -10 is 10 degree units below zero. We can record positive and negative numbers easily by setting up a number line.

-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----
-10 -8 -6 -4 -2 0 +2 +4 +6 +8 +10

Signed numbers are positive (+4 or 4) or negative (-4) and have two parts: magnitude (4) and direction (+ or - ). All numbers to the right of zero on the number line are positive; all numbers to the left are negative. Operations with signed numbers can be represented by movement on the number line.

There are several different approaches to calculations using positive and negative numbers. Two, rather different approaches are presented below. Try them both and use the one that works best for you.

METHOD #1

Addition & Subtraction

STEP 1: Always simplify your work by removing as many "extra" signs as possible. Replace any number in the form - (-n) with +n or simply n. Replace any number in the form of +(-n) or - (+n) with simply -n.

(-8) = +8 or 8 +(-2) or - (+2) = -2

STEP 2: If two numbers that you're combining (adding or subtracting) have the same sign, find the sum and apply that same sign to your answer.

+8 + 2 = +10 = 10
- 8 + (-2) = - 8 - 2 = -10
- 8 - (+2) = - 8 - 2 = -10

STEP 3: If the two numbers you're combining have different signs, find the difference between the two numbers and apply the sign of the larger number to your answer.

+8 - 2 = +6 or 6

- 8 - (-2) = - 8 + 2 = - 6

Multiplication and Division

RULE: For any two numbers being multiplied or divided with the same sign, the result will always be positive. For any two numbers that you're multiplying or dividing with opposite signs, the result will always be negative.

4 × 2 = +8 (+) × (+) = (+)
-4 × 2 = -8 (-) × (-) = (-)
-4 × -2 = 8 (-) × (-) = (+)
(2)(-3)(4)(-1) = (-6) x (-4) = +24 or 24

Any odd number of negative terms, multiplied or divided, will result in a negative answer. Any even number of negative terms, multiplied or divided, will result in a positive answer.

METHOD #2

Addition

Ask yourself if the signs of the numbers you're adding are alike or different. If signs are alike, add the digits, keep the same sign in your answer. If the signs are different, subtract the smaller digit from the larger digit, use the sign of the larger for your answer.

Subtraction

Rewrite all subtraction problems as equivalent addition problems by adding the opposite, e.g., a - b = a + (-b) This phrase says "positive a minus positive b equals positive a plus negative b." Then follow the rules for addition of signed numbers.

-3 - 5 = -3 + (-5) = -8
8 - (-3) = 8 + 3 = 11
-12 - (-5) = -12 + 5 = -7

Multiplication & Division

First, ask yourself if the signs of the numbers are alike? If so, your answer will be positive. In multiplication and division of signed numbers, like signs = a positive result. Are the signs different? If so, your answer will be negative. Different signs = a negative result.

Reference:
http://lac.smccme.edu/signed_numbers.htm

Simplifying Fractions

To simplify a fraction, divide the top and bottom by the highest number that

can divide into both numbers exactly.

Simplifying Fractions

Simplifying (or reducing) fractions means to make the fraction as simple as possible. Why say four-eighths (4/8) when you really mean half (1/2) ?

4/8 (Four-Eights)



2/4(Two-Quarters)



1/2(One-Half)










How do I Simplify a Fraction ?
There are two ways to simplify a fraction:

Method 1
Try dividing both the top and bottom of the fraction until you can't go any further (try dividing by 2,3,5,7,... etc).

Method 2
Divide both the top and bottom of the fraction by the Greatest Common Factor, (you have to work it out first!).

Fractions may have numerators and denominators that are composite numbers (numbers that has more factors than 1 and itself).

How to simplify a fraction:

1.Find a common factor of the numerator and denominator. A common factor is a number that will divide into both numbers evenly. Two is a common factor of 4 and 14.

Divide both the numerator and denominator by the common factor.

Repeat this process until there are no more common factors.
The fraction is simplified when no more common factors exist.
Another method to simplify a fraction

2.Find the Greatest Common Factor (GCF) of the numerator and denominator
Divide the numerator and the denominator by the GCF.


Operations in fractions

Multiplying Fractions
Multiplying two fractions is the easiest of any of the operations.

Rule for Multiplication of Fractions

When multiplying fractions, you simply multiply the numerators together and then multiply the denominators together. Simplify the result.

This works whether the denominators are the same or not.

So, if you wish to multiply the fractions 3/2 and 4/3 together you get 12/6.

As with any solution, you should report the answer in simplified form. The fraction 12/6 can be simplified to 2.

You should recall that any number divided by itself is 1, so 6/6=1. In other words, if you find the same number on both the top and the bottom of a fraction, you can cancel it out.

Example
What do you get when you multiply 1/2 and 3/7?

The result of multiplying these two fractions is 3/14.


The fraction 3/14 cannot be simplified any further; it is in its simplest form.

Dividing Fractions

Dividing one fraction by another is almost as easy as multiplying two fractions. It even involves multiplying fractions! First, let's look at how division of two fractions may be represented. If we wish to divide 3/5 by 2/3, we could write that as:

or

Rule for Division of Fractions

When you divide two fractions, you take the reciprocal of the second fraction, or bottom fraction, and multiply. (Taking the reciprocal of a fraction means to flip it over.)

As with multiplication, this works whether the denominators are the same or not.

So, if you wish to divide the fraction 3/2 by 4/3, you get the result shown at the right. As with any solution, you should report the answer in its simplified form. In this case, 9/8 is in its simplest form.

Example
What do you get when you divide 12/17 by 6/7?
The answer is 14/17.

We take the reciprocal of the second fraction and multiplying it by the first. We get 82/102, which, however, is not in its simplified form.

One easy way to simplify this fraction is go back to the step before the numerator and denominator were multiplied.

To reduce a fraction to its simplest form, we need to find the prime factors of both the numerator and denominator (This was shown in the unit on Equivalent Fractions). When we do this for the numerator and denominator we find we can cancel out a 2 and a 3 from the top and bottom. This gives us the result 14/17.

Adding and Subtracting Fractions

When adding and subtracting fractions, the fractions being added or subtracted must have the same denominator. When denominators are different, you will need to convert each fraction into an equivalent fraction by finding the least common denominator (LCD) for the fractions. The two new fractions should have the same denominator, making them easy to add or subtract. (Determining the LCD of a set of fractions was reviewed in the unit Comparing Fractions.)

Rule for Addition of Fractions

When adding fractions, you must make sure that the fractions being added have the same denominator. If they do not, find the LCD for the fractions and put each in its equivalent form. Then, simply add the numerators of the fractions.

Rule for Subtraction of Fractions

When subtracting fractions, you must make sure that the fractions being subtracted have the same denominator. If they do not, find the LCD for the fractions and put each in its equivalent form. Then, simply subtract the numerators of the fractions.

This rule can be broken down into several steps:

1. Determine whether the fractions have the same denominator.

If the denominators are the same, move to step 4.
2. If the denominators are different, find the LCD for the fractions being added.
3. Find the equivalent fractions with the LCD in the denominator.
4. Add or subtract the numerators of the fractions.
5. Simplify the resulting fraction.

1. If we have the fractions 1/6 and 2/6, and wish to add them, we follow our steps:
4. Determine whether the fractions have the same denominator. If the denominators are the same, move to step 4.
5. Simplify the resulting fraction. This fraction can be simplified to 1/2.
The fractions 1/6 and 2/6 have the same denominator, so we can move to step 4.

Visually, this would look like:

Now let's try an example.

Example of Adding Fractions

What is the sum of 3/4 and 1/3?
The answer is 13/12.

Following the steps:

1. Determine whether the fractions have the same denominator.
If the denominators are the same, move to step 4.
First, you should notice that the two fractions do not have the same denominator. This means we need to find the LCD for the two fractions.

2. Find the LCD for the fractions being added.
a. Write the prime factors for the denominator of each fraction.
The prime factors of 4 are: 2 and 2.
The prime factor of 3 is: 3

2. Note all prime factors that occur. For each prime factor that occurs, determine in which denominator it occurs the most. Write down the prime factor the number of times it occurs in that one denominator.
The prime factors that occur are 2, 2, and 3.

3. Calculate the LCD of your fractions. To do this, multiply the factors selected in step 2b.
2 x 2 x 3= 12,
12 is our LCD.

4. Find the equivalent fractions that have the LCD in the denominator.

Let's start with 3/4. The prime factor missing from this denominator is a 3. So, 3 is the multiplier for 3/4.


For the fraction 1/3, the prime factors that are missing are 2 and 2. Since 2 x 2= 4, 4 is the multiplier for the fraction 1/3.


Add the numerators of the fractions.

Now that we have found the fractions that are equivalent to the ones we are adding, and these have the same denominator, we can add the fractions together.

We can see that the fraction we are adding are 9/12 and 4/12, which equals 13/12.


5. Simplify the resulting fraction.
The answer of 13/12 is in its simplest form.

The steps for subtracting fractions are the same as for addition. The only difference is substituting subtraction for addition. If we wish to subtract 1/8 from 4/8, we can follow the steps outlined above.

1. Determine whether the fractions have the same denominator. If the denominators are the same, move to step 4.
They are the same, so we can skip to step 4.

4. Subtract the numerators of the fractions.


5. Simplify the resulting fraction.
This fraction, 3/8, is in its simplest form.

As you can see, addition and subtraction of fractions is similar to adding and subtracting whole numbers. The important point is to be sure the fractions being added or subtracted have the same denominator.

Reference:
http://www.mathsisfun.com/simplifying-fractions.html
http://www.aaamath.com/fra66h-simpfrac.html
http://cstl.syr.edu/FIPSE/fracunit/Opfrac/Opfrac.htm