Seminar in Mathematics: Radical

Radical, from Late Latin radicalis "of roots" and from Latin radix "root", may refer to:radical symbol (√), a symbol used to indicate the square root or nth root.

A radical
or the principal nth root of k:
k, the radicand, is a real number.
n, the index, is a positive integer greater than one.

Properties of radicals:

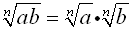
Simplifying Radicals:

Radicals that are simplified have:
- no fractions left under the radical.
- no perfect power factors in the radicand, k.
- no exponents in the radicand, k, greater than the index, n.
- no radicals appearing in the denominator of a fractional answer.

Examples:

Simplify: Factor the radicand to isolate the perfect power factor(s), which will allow them to be removed from under the radical. You will need to remember your rules for working with exponents in order to isolate the perfect powers.

(notice the perfect cube of 8 being isolated)

(in this problem, several perfect squares were isolated, namely 9, a^2 and b^4)

(the -8 and the y^3 are perfect cubes)

(x^5 is a perfect power of 5)

perfect squares
4, 9, 16, 25, 36, ...
x^2, x^4, x^6, x^8, ...
x^2y^2, x^2y^4, 16x^6y^8, ...powers are "even"

perfect cubes
8, 27, 64, 125, ...
x^3, x^6, x^9, x^12, ...
x^3y^3, x^3y^6, 27x^6y^9, ...powers are "multiples of 3"

To add radicals,simplify first if possible, and add "like" radicals.

(After simplifying the radicals, it became apparent which radicals could be added.)

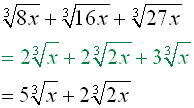
(Be sure to combine ONLY like radicals.Also be sure to continue writing the index of 3.Failing to do so, creates an incorrect answer using square root, instead of the correct cube root.)

To multiply radicals apply

and/or distributive multiplication (FOIL)

(multiply outside, multiply inside, and simplify)

(notice the perfect powers isolated)

(distribute across the parentheses)

(this problem requires multiplication of two binomials by distributive multiplication or FOIL. Notice how none of the terms can be combined in the final answer.)

(again binomial multiplication is needed. This time, however, terms can be combined for the final answer.)

(again binomial multiplication is needed. The two terms being multiplied in this problem are conjugates. Notice how the middle terms of the answer drop out.)

"Roots" (or "radicals") are the "opposite" operation of applying exponents; you can "undo" a power with a radical, and a radical can "undo" a power. For instance, if you square 2, you get 4, and if you "take the square root of 4", you get 2; if you square 3, you get 9, and if you "take the square root of 9", you get 3:

You can raise numbers to powers other than just 2; you can cube things, raise them to the fourth power, raise them to the 100th power, and so forth. In the same way, you can take the cube root of a number, the fourth root, the 100th root, and so forth. To indicate some root other than a square root, you use the same radical sybmol, but you insert a number into the radical, tucking it into the "check mark" part. For instance:

Simplifying Square-Root Terms

To simplify a square root, you "take out" anything that is a "perfect square"; that is, you take out front anything that has two copies of the same factor:

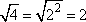
Sometimes the argument of a radical is not a perfect square, but it may "contain" a square amongst its factors. To simplify, you need to factor the argument and "take out" anything that is a square; you find anything you've got a pair of inside the radical, and you move it out front. To do this, you use the fact that you can switch between the multiplication of roots and the root of a multiplication. In other words, radicals can be manipulated similarly to powers: