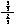Probability is a way of expressing knowledge or belief that an event will occur or has occurred. The concept has been given an exact mathematical meaning in probability theory, which is used extensively in such areas of study as mathematics, statistics, finance, gambling, science, and philosophy to draw conclusions about the likelihood of potential events and the underlying mechanics of complex systems.
Let's see how it could be defined on the simplest sample space of a single coin toss, {H, T}.
The two element sample space {H, T} has four subsets:
Φ = {}, {H}, {T}, {H, T} = Ω.
To be a probability, a function P defined on this four sets must be non-negative and not exceeding 1. In addition, on the two fundamental sets Φ and Ω it must take on the prescribed values:
P(Φ) = 0 and P(Ω) = 1.
The values P({H}) and P({T}) which we shall write more concisely as P(H) and P(T) must be somewhere in-between. P(H) is expected to be the probability of a coin landing heads up; P(T) should be the probability of its landing tails up. This is up to us to assign those probabilities. Intuitively those numbers should be expressing our notion of certainty with which the coin lands one way or the other. Since, for a fair coin, there is no way to prefer one side to the other, the most natural and common way is to make the two probabilities equal:
(1) P(H) = P(T).
As in real life, the choices we make have consequences. Once we decided that the two probabilities are equal, we are no longer at liberty to choose their common value. The definitions take over and dictate the result. Indeed, the two events {H} and {T} are mutually exclusive so that a probability function should satisfy the additivity requirement:
(2)
P({H}) + P({T}) = P({H} {T})
= P({H, T})
= P(Ω)
= 1.
The combination of (1) and (2) leads inevitably to the conclusion that a probability function that models a toss of a fair coin is bound to satisfy P(H) = P(T) = 1/2.
Two events that have equal probabilities are said to be equiprobable. It's a common approach, especially in the introductory probability courses, to define a probability function on a finite sample space by declaring all elementary events equiprobable and building up the function using the additivity requirement. Having a formal definition of probability function avoids the apparent circularity of the construction hinted at elsewhere.
Let's consider the experiment of rolling a die. The sample space consists of 6 possible outcomes
{1, 2, 3, 4, 5, 6}
which, with no indication that the die used is loaded, are declared to be equiprobable. From here, the additivity requirement leads necessarily to:
P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 1/6.
Since all 6 elementary events - {1}, {2}, {3}, {4}, {5}, {6} - are mutually exclusive, we may readily apply the required additivity, for example:
P({1, 2}) = P({1}) + P({2}) = 1/6 + 1/6 = 1/3
and similarly
P({4, 5, 6}) = P({4}) + P({5}) + P({6}) = 1/6 + 1/6 + 1/6 = 1/2
Note that a 2-element event {1, 2} has the probability of 1/3 = 2·1/6, whereas a 3-element event {4, 5, 6} has the probability of 1/2 = 3·1/6.
Let X be the random variable associated with the experiment of rolling the dice. The introduction of a random variable allows for naming various sets in a convenient manner, e.g.,:
{1, 2} = {x: x <> 3) = 1/2.
Here are a few additional examples:
P({2, 4, 6}) = P(X is even) = 1/2,
P({1, 2, 4, 5}) = P(X is not divisible by 3) = 2/3,
P({2, 3, 5}) = P(X is prime) = 1/2.
In general, if an event A has m favorable elementary outcomes, the additivity requirement implies P(A) = m/6. In other experiments, with n possible equiprobable elementary outcomes, we would have P(A) = m/n.
For example, under normal circumstances, drawing a particular card from a deck of 52 cards is assigned a probability of 1/52. Drawing a named (A, K, Q, J) card (of which there are 4×4 = 16 cards) has a probability of 16/52. The event of drawing a black card has the probability of 26/52 = 1/2, that of drawing a hearts the probability of 13/52 = 1/4 and the probability of drawing a 10 is 4/52 = 1/13.
Later on, we shall have examples of sample spaces where considering the elementary events as equiprobable is unjustified. However, whenever this is possible, the evaluation of probabilities becomes a combinatorial problem that requires finding the total number n of possible outcomes and the number m of the outcomes favorable to the event at hand. It is then natural that properties of combinatorial counting have bearings on the assignment and evaluation of probabilities.
When tossing two distinct (say, first and second) coins there are four possible outcomes {HH, HT, TH, TT} and no reason to declare one more likely than another. Thus each event is assigned the probability of 1/4. Here are more examples
P({H popped up at least once}) = P({HH, HT, TH}) = 3/4,
P(First coin came up heads) = P({HH, HT}) = 2/4 = 1/2,
P(Two outcomes were different) = P({HT, TH}) = 2/4 = 1/2.
We consider tossing two coins as completely independent experiments, the outcome of one having no effect on the outcome of the other. It follows then from the Sequential, or Product, Rule that the size of the sample space of the two experiments is the product of the sizes of the two sample spaces and the same holds of the probabilities. For example,
P({HT}) = 1/4 = 1/2·1/2 = P({H})·P({T}).
More generally, given two sample spaces S1 and S2 with the number of equiprobable outcomes n1 and n2 and two events E1 (on S1) and E2 (on S2) with the number of favorable outcomes m1 and m2. Then P(E1) = m1/n1 and P(E2) = m2/n2. The sample space of two successive experiments has a sample space with n1n2 outcomes. The event E1E2 which occurs if E1 took place followed by E2 taking place consists of m1m1 favorable outcomes so that
P(E1E2) = m1m2/n1n2 = m1/n1 · m2/n2 = P(E1)P(E2).
The two coins may be indistinguishable and, when thrown together, may produce only three possible outcomes {{H, H}, {H, T}, {T, T}} where the set notations are used to emphasize that the order of the outcomes of the two coins is irrelevant in this case. However, assigning each of the elementary events the probability of 1/3 is probably a bad choice. A more reasonable assignment is
P({H, H}) = 1/4,
P({H, T}) = 1/2,
P({T, T}) = 1/4.
Why? This is because the results of the two experiments won't change if we imagine the two coins different, say if we think of them as being blue and red. But, for different coins, the number of elementary events is 4, with two of them - HT and TH - destined to coalesce into one - {H, T} - when we back off from our fantasy. The other two - HH and TT - will still have the probabilities of 1/4 and the remaining total of 1/2 should be given to {H, T}.
When rolling two die, the sample space consists of 36 equiprobable elementary events each with probability 1/36. The possible sums of the two die range from 2 through 12 and the number of favorable events can be observed from the table below:

Using S for the random variable equal to the sum of the two die, the additivity requirement leads to the following probabilities:
P(S = 2) = 1/36,
P(S = 3) = 2/36 = 1/18,
P(S = 4) = 3/36 = 1/12,
P(S = 5) = 4/36 = 1/9,
P(S = 6) = 5/36,
P(S = 7) = 6/36 = 1/6,
P(S = 8) = 5/36,
P(S = 9) = 4/36 = 1/9,
P(S = 10) = 3/36 = 1/12,
P(S = 11) = 2/36 = 1/18,
P(S = 12) = 1/36,
Note that the events are mutually exclusive and exhaustive: their probabilities add up to 1.
(As a curiosity, note that, say, both sums of 4 and 5 come up in two ways, viz., 4 = 1 + 3, 4 = 2 + 2, 5 = 1 + 4, and 5 = 2 + 3. However, as we just saw, P(S = 4) < s =" 5).">
Let's return to throwing a dice. (For an historic example, see the Chevalier de Méré's Problem.) With 3 die, the sample space consists of 8 = 23 possible outcomes. Four 4 die the number grows to 16 = 24, and so on. We obtain a curious sample space tossing the coin until the first tail comes up. The probability P(T) that it will happen on the first toss equals 1/2. The probability P(HT) that it will happen on the second toss is evaluated under the assumption that the first toss showed heads, for, otherwise, the experiment would have stopped right after the first stop. The the outcome of the first toss has no effect on the outcome of the second,
P(HT) = P(H)·P(T) = 1/2 · 1/2 = 1/4.
Continuing in this way, P(HHT) = 1/2·1/2·1/2 = 1/8 is the probability of getting the tails on the third toss; P(HHHT) = 1/16 is the probability of getting the tails on the fourth toss, and so on. The events are mutually exclusive and exhaustive:
P(T) + P(HT) + P(HHT) + ... = 1/2 + 1/4 + 1/8 + ...
= 1/2·1 / (1 - 1/2)
= 1,
as the sum of a geometric series starting at 1/2 with the factor also of 1/2.
This is a curiosity because there is one event that has been left over: this is the event in which the outcome T never occurs. An infinite number of coin tosses is called for, each with the outcome of heads: HHHH ... Although abstractedly this event is complementary to the possibility of having a tails in a finite number of steps, this event is practically impossible because it requires an infinite number of coin tosses. Deservedly it is assigned the probability of 0.
The probability that tails will show up in four tosses or less equals
P(T) + P(HT) + P(HHT) + P(HHHT) = 1/2 + 1/4 + 1/8 + 1/16
= 1/2·(1 - 1/24)/ (1 - 1/2).
More generally, the probability that the tails will show up in at most n tosses equals to the sum
1/2 + 1/4 + 1/8 + ... + 1/2n = 1/2·(1 - 1/2n)/ (1 - 1/2).
The interpretation of the infinite sum 1/2 + 1/4 + 1/8 + ... is that this is the probability of the tails showing up in a finite number of steps. This probability is 1 so that one should expect to get the tails sooner or later. For this sample space, an event with probability 0 is conceivable but practically impossible. In continuous sample spaces, events with probability 0 are a regular phenomenon and far from being impossible.
The game of poker has many variants. Common to all is the fact that players get - one way or another - hands of five cards each. The hands are compared according to a predetermined ranking system. Below, we shall evaluate probabilities of several hand combinations.
Poker uses the standard deck of 52 cards. There are C(52, 5) possible combinations of 5 cards selected from a deck of 52: 52 cards to choose the first of the five from, 51 cards to choose the second one, ..., 48 to choose the fifth card. The product 52×51×50×49×48 must be divided by 5! because the order in which the five cards are added to the hand is of no importance, e.g., 7♣8♣9♣10♣J♣ is the same hand as 9♣7♣10♣J♣8♣. Thus there are C(52, 5) = 2598960 different hands. The poker sample space consists of 2598960 equally probable elementary events.
The probability of whichever hand is naturally 1/2598960. [Mazur, pp. 81-82] shows another elegant way of arriving at the same probability. Imagine having a urn with 52 balls, of which 5 are black and the remaining white. You are to draw 5 balls out of the urn. What is the probability that all 5 balls drawn are black?
The probability that the first ball is black is 5/52. Assuming that the first ball was black, the probability that the second is also black is 4/51. Assuming that the first two balls are black, the probability that the third is black is 3/50, ... The fifth ball is black with the probability of 1/48, provided the first 4 balls were all black. The probability of drawing 5 black balls is the product:
The highest ranking poker hand is a Royal Flush - a sequence of cards of the same suit starting with 10, e.g., 10♣J♣Q♣K♣A♣. There are 4 of them, one for each of the four suits. Thus the probability of getting a royal flush is 4/2598960 = 1/649740. The probability of getting a royal flush of, say, spades ♠, is of course 1/2598960.
Any sequence of 5 cards of the same suit is a straight flush ranked by the highest card in the sequence. A straight flush may start with any of 2, 3, 4, 5, 6, 7, 8, 9, 10 cards and some times with an Ace where it is thought to have the rank of 1. So there are 9 (or 10) possibilities of getting a straight flush of a given suit and 36 (or 40) possibilities of getting any straight flush.
Five cards of the same suit - not necessarily in sequence - is a flush. There are 13 cards in a suit and C(13, 5) = 1287 combinations of 5 cards out of 13. All in all, there are 4 times as many flush combinations: 5148.
Four of a kind is a hand, like 5♣5♠5♦5♥K♠, with four cards of the same rank and one extra, unmatched card. There are 13 combinations of 4 equally ranked cards each of which can complete a hand with any of the remaining 48 cards. Giving the total of 13×48 = 624 possible "four of a kind" combinations.
A hand with 3 cards of one rank and 2 cards of a different rank is known as Full House. For a given rank, there are C(4, 3) = 4 ways to choose 3 cards of that rank; there 13 ranks to consider. There are C(4, 2) = 6 combinations of 2 cards of equal rank, but now only 12 ranks to choose from. There are then 4×13×6×12 = 3744 full houses.
A straight hand is a straight flush without "flush", so to speak. The card must be in sequence but not necessarily of the same suit. If the ace is allowed to start a hand, there are 40 ways to choose the first card and then, we need to account that the remaining 4 cards could be of any of the 4 suits, giving the total of 40×4×4×4×4 = 10240 hands. Discarding 40 straight flushes leaves 10200 "regular" flushes.
Three of a kind is a hand, like 5♣5♠5♦7♥K♠, where three cards have the same rank while the remaining 2 differ in rank between themselves and the first three. There are 13×C(4, 3) = 52 combinations of three cards of the same rank. The next card could be any of 48 and the fifth any of 44 and the pair could come in any order so the products needs to be halved: 52×48×44 / 2 = 54912.
There remain Two pair and One pair combinations that are left as an exercise.
Reference;
http://www.cut-the-knot.org/probability.shtml
http://en.wikipedia.org/wiki/Probability


 where
where









 is actually an integer.
is actually an integer.